Visualizing the Monty Hall Problem

Originally written on 2009 April.

This is a famous thing from the advanced annals of mathematics again.  Luckily there is very little mathematical debate on this, but at a time — there used to be.

However, this is a problem that many people (including me) have trouble visualizing, so they just choose to memorize the answer and forget about it.  This is the Monty Python Hall Problem.

Here’s the problem in case you’re not familiar with it:

Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?

– Parade Magazine, 1990

And of course the solution:

Because there is no way for the player to know which of the two remaining unopened doors is the winning door, most people assume that each of these doors has an equal probability and conclude that switching does not matter. In fact, the player should switch—doing so doubles the probability of winning the car from 1/3 to 2/3.

But then the real question — why?

The Real Clear Reason

The reason is explained best like this:

• There are three doors.  Two contain goats, one contains a nice cartoon car.
• You pick a door.
• Monty Hall reveals another door.  This is one of the two goats.
• Probability says it’s most likely that you picked a goat. (2/3 chance of goat, since there are two goats and three doors.
• Switching will likely not switch to a goat, because you won’t switch to the door you already have (goat) and you won’t switch to the revealed door (goat), so the only other door is the one most likely to be a car.

Since there were three doors and one car, you only had a 1/3 chance of starting on a car.  Since the other two doors have an end result of a car, you have a 2/3 chance of getting the car if you switch.

However…

Like most math problems, this is better understood through the power of pictures.  Remember, a picture is worth a thousand words.  And if that picture is the Portrait of Adele Bloch-Bauer I, that means a word is worth approximately $135,000.  Which means I could sell this paragraph for roughly $7,155,000.  Want to buy it?

First, you pick a door.

Even though the doors appear open, the goats and car are hidden behind the awesome clipart swirl.

You have a 1/3 chance of picking the car, given any door you pick.

Door #1: You pick a goat, but don’t know it.

While you don’t know for sure because you don’t really see what is behind the non-revealed doors, this is the time you would want to switch.  If you switch you get the car.

If you stay, you get the goat.

Door #2: You pick the car, but don’t know it.

Again, you don’t actually know what is behind the doors.  But in this circumstance, this is where you don’t want to switch.  If you switch, you get the goat.  Goats are harder to care for then cars… well, most cars.  Also they have less retail value than cars… well, most cars.  Either way, the point of the problem is to avoid getting a goat.  So don’t switch.

If you stay, you get the car.  Woot.

Door #3: You pick a goat, but don’t know it.

If you switch you get the car. :)

If you stay, you get the goat. :(

A summary table!

Notice that staying on your door results in a car one-third of the time, whereas switching results in a car two-thirds of the time.

Here is another really good summary image.  It was lovingly ripped off from Wikipedia:

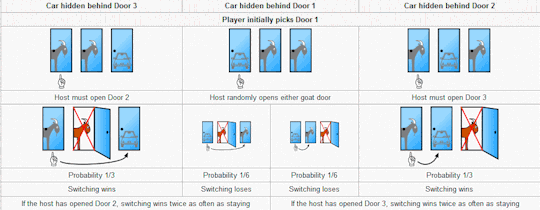
Well, that’s the Monty Hall Problem

…and that’s why switching results in the car two-thirds of the time.  Now that you’ve figured out the Monty Hall Problem, maybe you could go on to the Two Envelopes Problem.